Presenters: Neel, Prof. T
Resources:
Computational Constructions in 3D
Primitives:

Scalar s = <x>
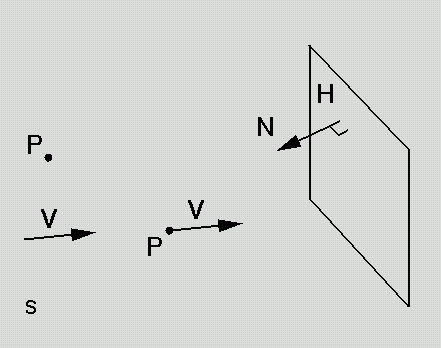
Point P = <x, y, z>
Vector V = <x, y, z>
Plane H = <A,
B, C, D> = <N, D>
H(P) = N.P
+ D = scalar function
Plane is zero set of this function.
[Note
halfspaces H+, H-.]
What is plane normal? Why?
Ray R
= <P, V>
I.e., a point and a direction
Operators/Constructors:
[Conventions ? Failure cases ?]
Length
(L2 norm) of vector V:
L(V)= |V| = sqrt(V.x^2
+ V.y^2 + V.z^2)
(Note C-like "." operator for accessor)
Vector V from P to Q: V = Q - P
Unit vector V' = V/L(V) = Unit(V)
Plane H normal to unit vector
N, containing point P
H.N = N
H.D = ?
Arithmetic argument:
H(P) = 0 = N.P
+ D
D by inspection.
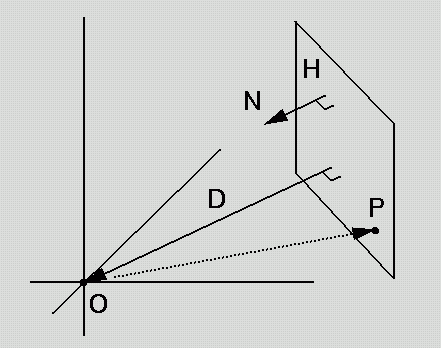
Geometric argument:
Interpret P as vector from
origin
Express altitude D in terms
of P, N
(what
is known about D, N ?)
D = -N(N.P),
D = -|D| by inspection.
Summary of Plane constructors:
[Conventions ? Failure cases
?]
Four scalars
(Unit) Vector, scalar
Vector, point
Three points
Two vectors, one point
Two points, one vector
[two interpretations]
Notation:
Inner product . : N.P (scalar)
Cross product x : N x P (vector)
Flat (concatenation): PQ (subspace)
Intersection ^ : PQ
^ H (subspace)
Operators:
0) Signed distance of P from plane <N,D>
H.P = N.P + D [note abusive notation]
1) Intersect ray <R,V> with plane <N,D>
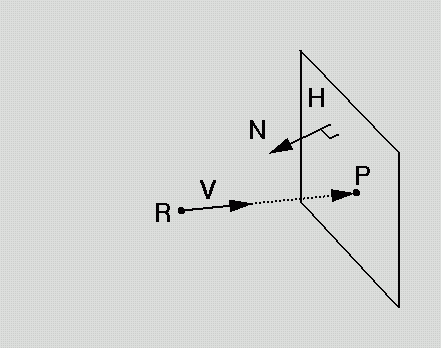
Ray is parametric: P(t) = R
+ t V
Plane is implicit: H.P(t)
= 0
Solve for t which satisfies both:
H.P(t) = (N.R + t N.V) + D = 0
t = -(N.R + D)/N.V
What is intersection point ?
2) Intersect ray <R,V> with sphere <C,r>
Ray is parametric: P(t) = R + tV
Sphere is implicit: (P-C).(P-C) = r2
Solve for t which satisfies both:
(R + tV - C).(R + tV - C) = r2
t = ...
3) Nearest pt P on sphere to given ray?
There is a closed form solution. But...
there is also a much easier way - what?
Find point P "by construction"!
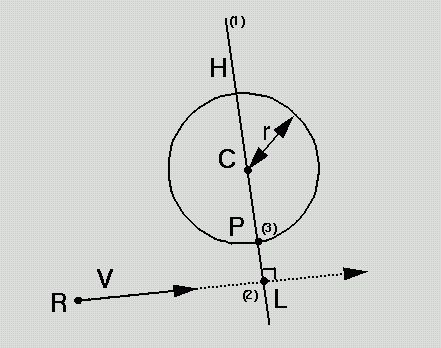
0) Given ray <R,V>; sphere <C,r>
1) Construct plane H from V, C
2) Intersect <R,V> with H to
find L
3) Intersect CL with sphere to find
P
Express in closed form as:
P = C + D UnitVector(C, L)
4) What is the nearest point on ray ?
4) Line-line (ray-ray) closest approach:
(Closed-form: parametrize in s,t;
minimize w.r.t. both parameters)
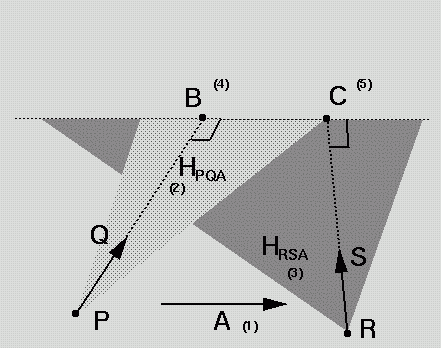
0) Given ray <P,Q>; ray <R,S>
1) Form A = Q x S
2) HPQA = Plane(P, Q, A)
3) HRSA = Plane(R, S, A)
4) B (on PQ) is PQ ^ HRSA
5) C (on RS) is RS ^ HPQA
And many others. But how to use them?
Examples, introduction to gvis.
Meeting 3 (Wednesday): Primitives, Duality [Marc]
Previous Meeting .... Next
Meeting ... Course Page
Last modified: Feb 1998
Seth Teller, MIT Computer Graphics Group, seth@graphics.lcs.mit.edu