Low-Dimensional Linear Programming

Presentation by: Marc Lebovitz

What is Linear Progamming?

Linear programming maximizing an objective function with respect to a given set of constraints.
An instance of an LP is defined as:
1. set of constraints: halfspaces H1->Hn
2. objective function: vector c
Here's a 1D Example:

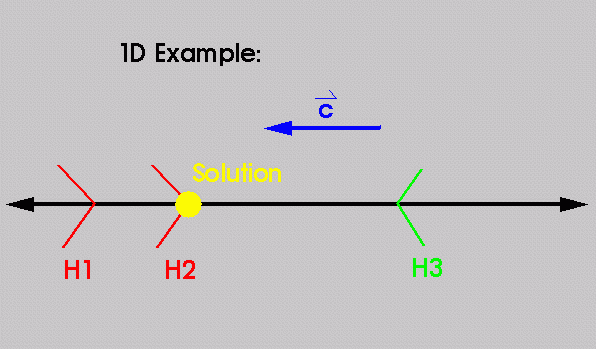The space is linear, parameterized on t.
Halfspaces are lower or upper bounds on t. They are represented by 2 #s: 1. value for t 2. max/min indicator
Objective Function is to maximize or minimize t, and can be represented by 1 #.
The solution, if it exists and is finite, must lie on either the maximum lower bound or the minimum upper bound.
Which should it lie on? Consult the objective function.

Why is this case infeasible? The maximum lower bound is greater than the minimum upper bound.

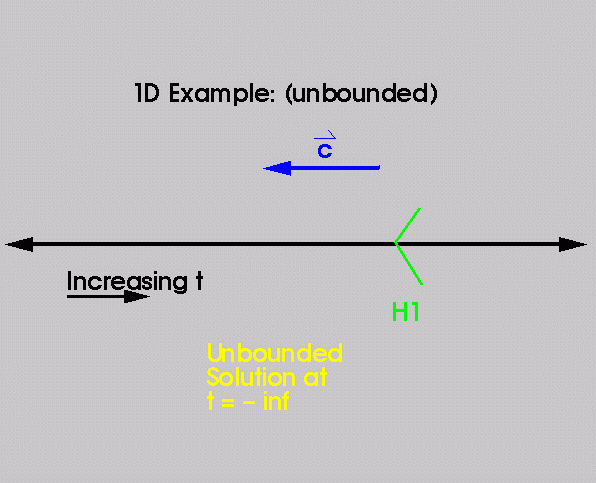This case is unbounded. There is no lower bound and the objective function is to minimize t.
Therefore, the solution is t = - Infinity.

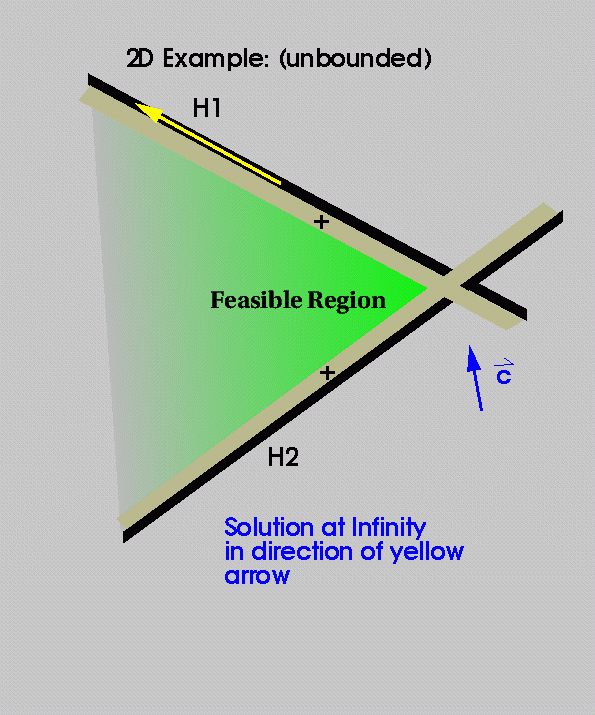
Now, let's move into 2 dimensions and see how we solve LP problems there:

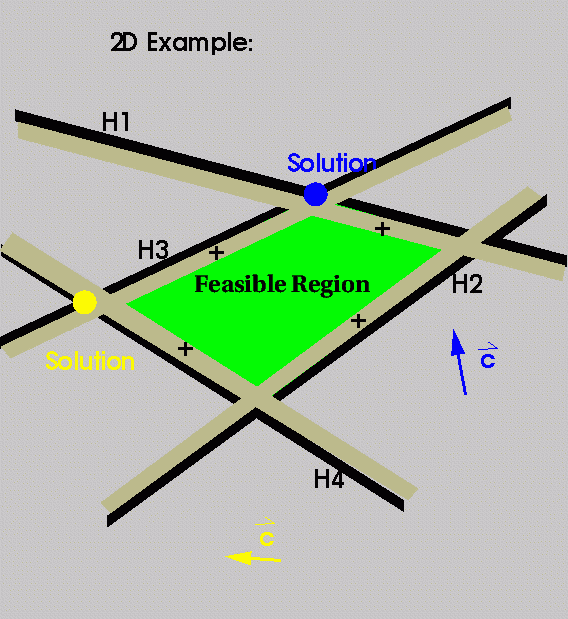Halfspaces are halfplanes and can be represented by 3 #s: A,B,C where Ax+By+C >= 0.
The objective function can be represented by 2 #s: vector c = (x,y)

In 3D, halfspaces are bounded by planes: Ax+By+Cz+D >= 0
objective function is a 3-vector: (x,y,z)

In d dimensions:
                            halfspace constraints are represented by d+1 #s:
                                     C₀*X_{0 +} C₁*X₁ + ... + C_d*X_d+ C_d+1>= 0
                            objective function is represented by d #s
                                     (F_0, F_1, ... , F_n)