Voxels representation & Marching Cubes Algorithm

Definition: A voxel is a volume element, typically a cubic cell.

The concept of isosurface

Potential function on voxels

The space being discretized, let every vertex of voxel have some numerical value (3D field of values) that we will call a potential.
As an example, consider in 2D a point, and for every vertex the distance to this point. Then a curve of constant potential (isocurve) is a circle.

This isosurface defines two regions: green vertices have a value under the threshold (potential of the isosurface), the others above.

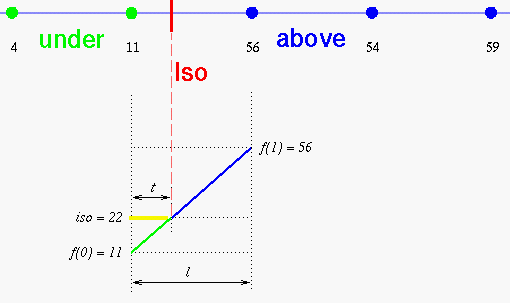
Linear interpolation for the isosurface location

Keeping only voxels that are fully inside (8 vertices) produce a jagged surface. The idea of the marching cubes algorithm is to slice the voxels intersecting with the isosurface. For that purpose, let us examine a 1D case.

The vertices are the green and blue points on top. We expect the isosurface to be around the red line by linear interpolation. How do we achieve this in 3D?

Marching cubes algorithm

Description and implementation details J. Sharman, D. Harvey.

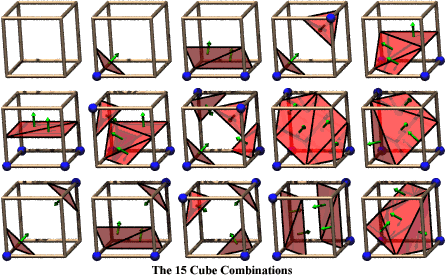
Every vertex of the voxel can be either under or above the threshold. There are 8 vertices for a cube, so we get 2⁸ = 256 possibilities.

However to simplify the algorithm we can reduce the complexity by taking into account cell combinations that duplicate under the following conditions.

Rotation by any degree over any of the 3 primary axis
Mirroring the shape across any of the 3 primary axis
Inverting the state of all corners and flipping the normals of the relating polygons.

Taking this into account we can resolve the original 256 combinations of cell state down to a total of 15 combinations (see below). The blue spheres denote corners that have been tested as inside the shape and the green arrows denote the surface normals of the relevant triangles.

Another representation of the combinations

Original paper: "Marching Cubes: A High Resolution 3D Surface Construction Algorithm", William E. Lorensen and Harvey E. Cline,
Computer Graphics (Proceedings of SIGGRAPH '87), Vol. 21, No. 4, pp. 163-169.

Improved Marching cubes for solving holes pb

Ambiguity which creates troubles with holes for instance.

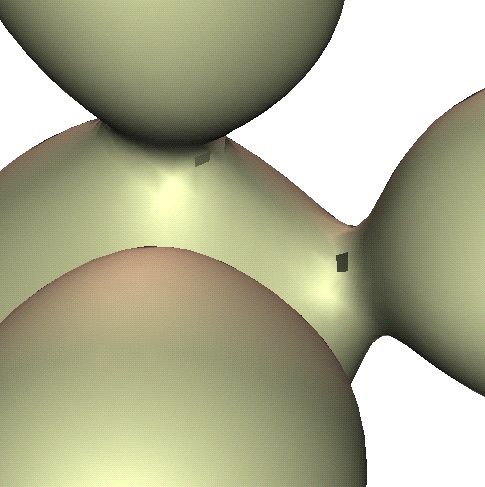
Consequently we have to consider 8 additional cases

Final smoothing

Due to the tradeoff computation time / resolution, the extracted surface has often to be smoothed:

What potential can we define at voxels vertices?

Density

Image of RNA granules inside oligodendrocyte using the Marching Cubes Algorithm

Distance to the surface...

...for a triangulated mesh (scanned object). Then look for threshold zero.

Thanks to Hans for his fantastic results: http://graphics.lcs.mit.edu/~hkp/

Further reading : Bloomenthal, Introduction to Implicit Surfaces, Morgan Kaufmann, 1997.

Eric Amram, Feb 1998, MIT 6.838 Advanced Topics in Computer Graphics - Prof. Seth Teller.