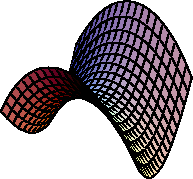Explicit and Implicit functions
What is a surface ?
Generally speaking, a surface is a subspace of codimension 1. In R3
for instance, a surface has dimension 2 and can be defined by two (well-chosen
!) parameters. We will not talk about fractals today.
How do we define a surface ?
Explicitly
Every point of the surface / volume is explicitly defined, for instance
by a function of some parameters. 
Implicitly
Points are not given directly: a condition states whether a point
belongs to the surface or not. For instance, points are solution of 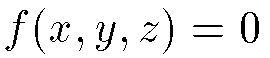
When f is polynomial, we dive into the field of algebraic geometry
(so don't get impressed by this word). Degree 1: plane, degree 2: quadric
surfaces (ellipsoid, paraboloid, hyperboloid, etc.)
-
Example: a sphere has both representations.
-
Some (quick) properties:
-
Jordan separation theorem : a closed surface separates R3
into two connected open sets, an interior and an exterior [generalization
to Rn].
-
The Implicit Function Theorem to be treated in a next lecture: the idea
is that under conditions of continuity and differentiability, you get z=g(x,y)
locally.
Manifolds : subspaces with maps
Every point has a neighborhood equivalent to a disk. In the case of differentiable
manifolds : at every point it exits a local map (a local referential
with same dimension as the manifold) and we go smoothly from one map to
another. This ensure for instance that at every point you can define texture
coordinates in a neighborhood. This obliges also the manifold not to have
holes or intersection of two edges (when it is bounded).
In our cases, there is most often a single map covering the whole surface.

Some Visual Examples
Height Fields
Defined by 


Ruled surfaces

Given a parameterized curve  and a sequence of unit vectors
and a sequence of unit vectors 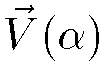 that varies continuously with alpha, the parametric
that varies continuously with alpha, the parametric
surface defined by  is called a ruled surface.
is called a ruled surface.
Click here for Equations.
Less formally, it is the surface swept out by
moving a straight line along the curve C so that it points in the direction
V for every alpha.
Examples :
but also
-
(Elliptic) Hyperboloid
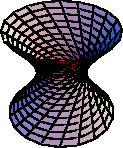
-
Hyperbolic Paraboloid (doubly ruled)
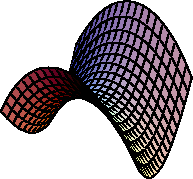

-
Plücker's Conoid

-
Möbius Strip

Surfaces of revolutions
A surface of revolution is a surface generated by
rotating a 2-D Curve about an axis
Click here for Equations.
-
Apple
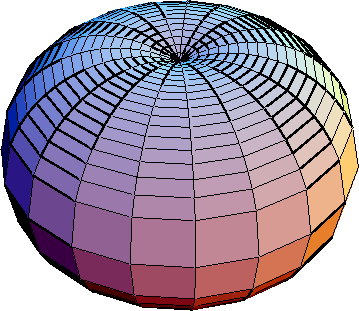
-
Gabriel's Horn

-
Torus

And much more to come !
Boy surface 
An excellent site to visit for the equations of
all the surfaces you can dream about is Eric's
Treasure Trove of Mathematics
Eric Amram, Feb 1998, MIT 6.838 Advanced Topics in Computer
Graphics - Prof. Seth Teller.

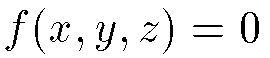
![]()




 and a sequence of unit vectors
and a sequence of unit vectors 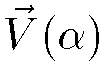 that varies continuously with alpha, the parametric
that varies continuously with alpha, the parametric
 is called a ruled surface.
is called a ruled surface.