
6.838 May 11 Meeting 25
Marek Teichmann
| 1. Definitions |
Def: Voronoi Diagram
partition of space into regions VR(s) s.t.
For all p in VR(s), d(p,s) < d(p,t)
for all t not = s.

Alternative Def:
Given 2 sites s,t,
the bisector B(s,t) of s and t is
the set of points p equidistant to s and t (generators)
Example: bisector of 2 points is a line.
Def: The dominance region of s over t is the set of points closer to s than t.
Example: dominance region of a point in a 2 point set is a half-space.
Def: Voronoi region VR(s):
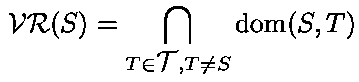
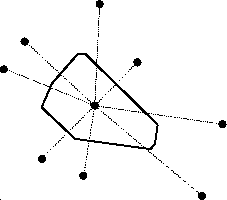
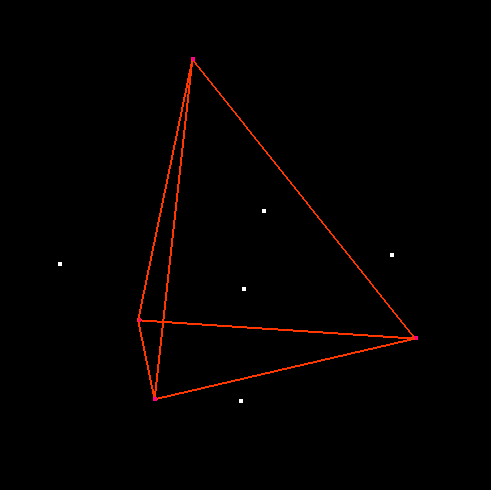
Question: How to find a vertex of VR(s) ?
Voronoi region of point in the center: (cross-eyed stereo pair)
 |
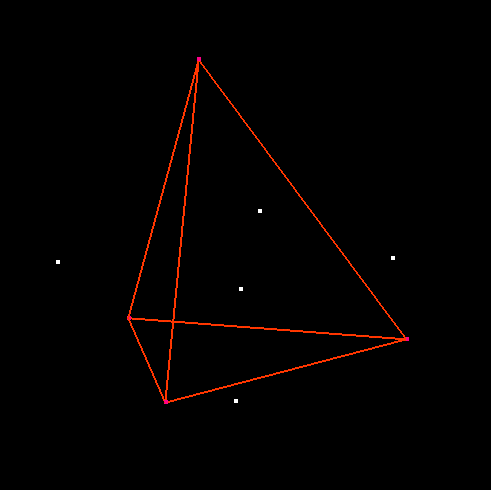
|
DT in 4D + duality (similar to 3D case)
Front propagation / prairie fire analogy.
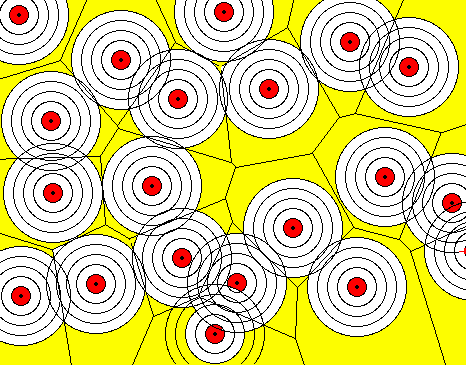 (J.
Smith, Oberlin).
(J.
Smith, Oberlin).
Prairie fire analogy
At time t the front (fire) is a set of circles of radius t.
Circles intersect at Voronoi edges.
What is the relation to the distance function?
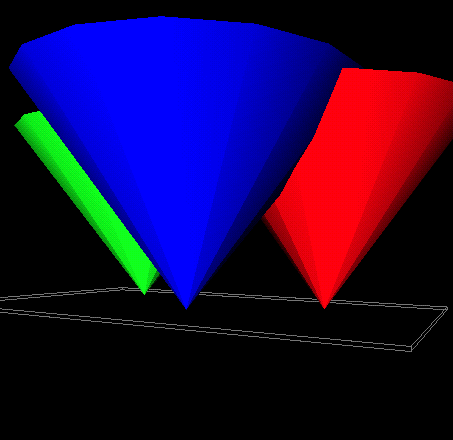 |
 |
<demo: SceneViewer 3cones2.iv>
Voronoi edges = ridges of distance function.
Take min of all distance cones --> graph of distance function
from all sites.
Generalizes to 3D.
| 2. Voronoi diagram of polygons & Medial Axis |
Geometry in action page (Eppstein)
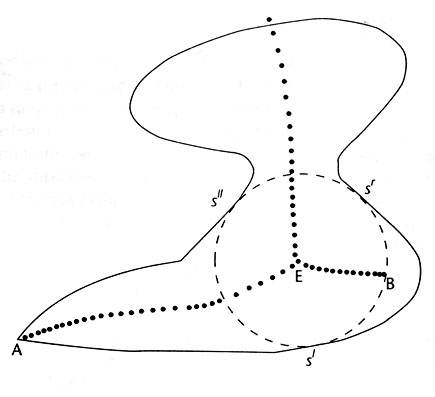
Set of points in space equidistant to 2 or more points on the surface (curve).
Examples:
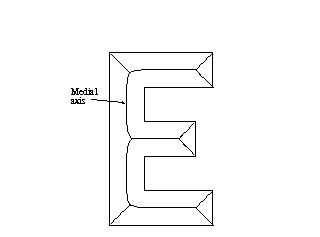 |
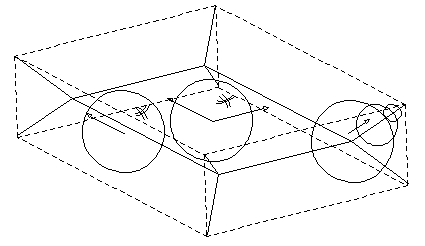 |
Set of edges.
Bisectors:
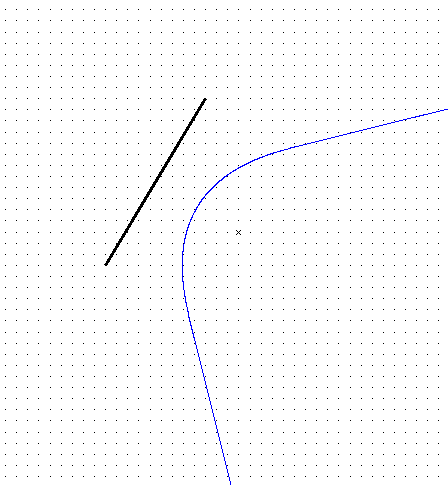 |
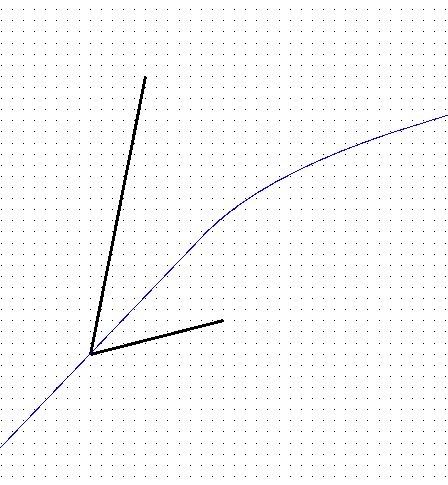 |
Voronoi diagram:
 |
 |
Note: Voronoi diagram of convex polygon is linear.
Problem: Voronoi edges not well defined by distance function

Solution 1: Use bisector of edges as above.
Problem: How to do this in 3D?
Solution 2: Add vertices as sites:
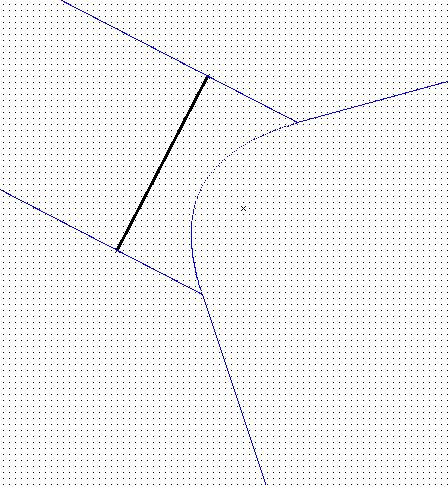 |
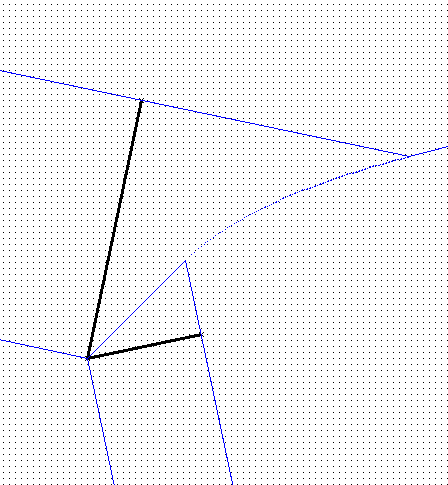 |
Advantage: a bisector now has only ONE mathematical definition (formula).
Corresponding Voronoi diagram:
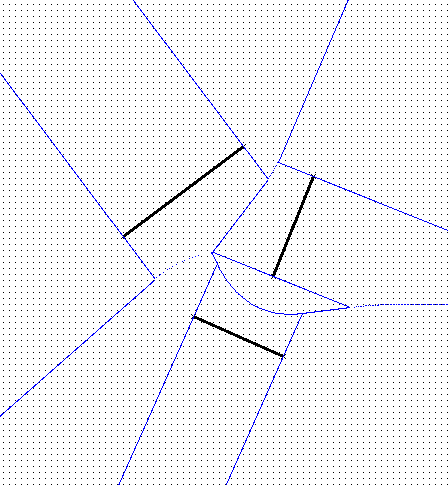 |
 |
Algorithm: incremental construction [Michael Seal, using LEDA]
HARD: why?
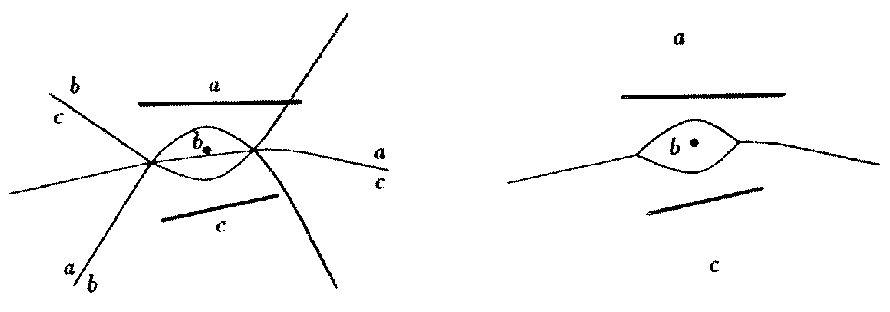
Insertion of point b into Voronoi diagram of segments a and
c
Intersection of quadratic curves, exact arithmetic...
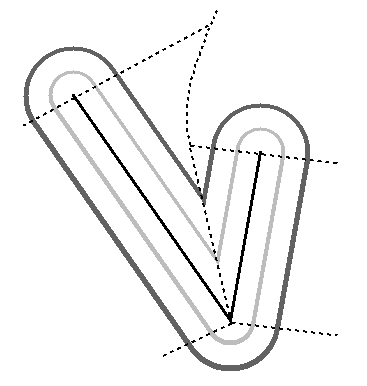
The medial axis is a subset of the Voronoi diagram of the edges and
vertices of the polygon.
Voronoi edges that meet the reflex vertices are not part of the medial
axis.
Bisectors:
| bisector type | portion of |
| point - point | plane |
| point - edge | parabolic cylinder |
| point - triangle | paraboloid |
| edge - edge | hyperbolic paraboloid |
| edge - triangle | parabolic cylinder |
| triangle - triangle | plane |
 |
 |
Edges:
Curves of algebraic degree <= 4.

Question: How to compute suface equidistant surface between 2 objects?
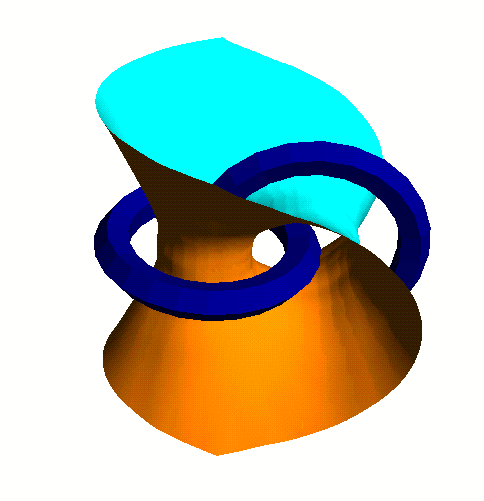
<demo vor>
| Algorithms for VD/MA of polyhedral objects |
No general exact algorithms for VD of triangles currently. Why?
--> use approximation algorithm!
Property: For convex polygonal objects, bisectors are linear.
Algorithm (based on wavefront idea):
Running time O(n2).
 |

|
 |
 |
<demo box>
 |
 |
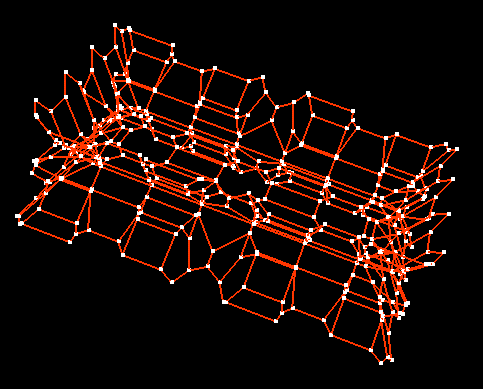
Use numerical technique to follow curve where fronts meet.
Computes skeleton of medial axis (edges, vertices).
[E. Sherbrooke, N. Patrikalakis, Solid Modeling 1995]
Drawback?
[Overmars et al.]
Idea:

Property: Cell C intersects Voronoi diagram if number of labels L(C) > 1
Question: Is this an iff?
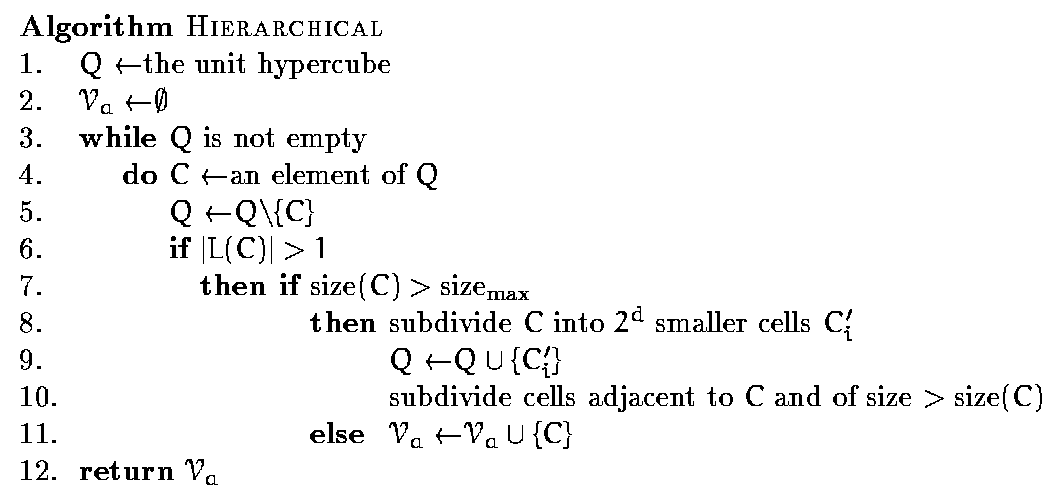
Examples.
3d Voronoi diagram skeleton of a set of tetrahedra (stereo pair):
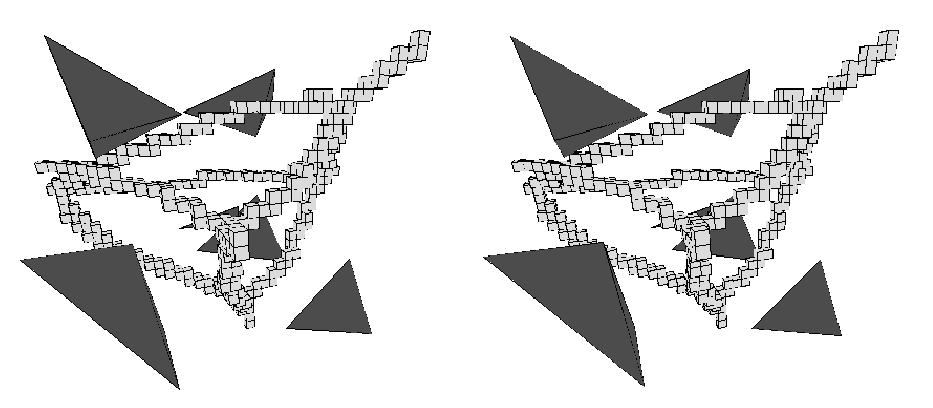
2d example showing hierarchical subdivision:
 |
 |
Use marching cubes-like algorithm for approximating Voronoi surfaces.
Use labels on corners:
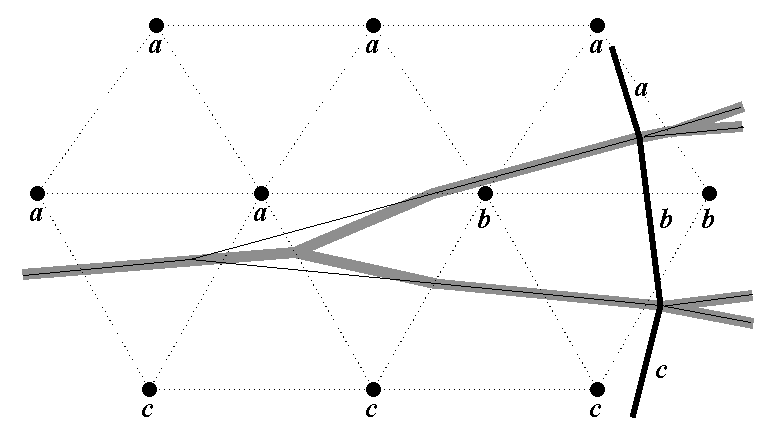
3D: Different cases for cell labels:

Dealing with cell labels.
Determine which Voronoi regions intersect cell.
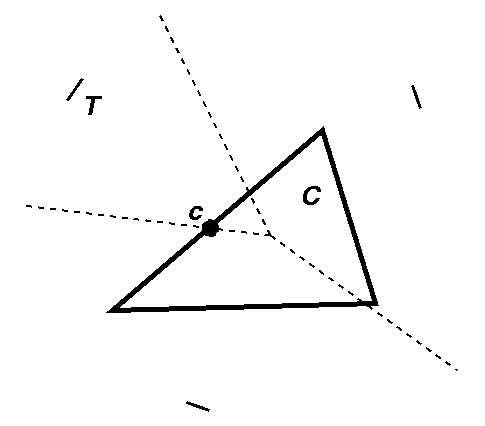
Fact [Teichmann & Teller]: Voronoi region of t intersects cell C iff point closest to t on C is closer to t than any other site.
Worst-case complexity of the medial surface of a polyhedron?
Upper bound is O(n3+e).
Lower bound example with Omega(n2) faces:

See Jeff Ericson's comments.
| Applications |
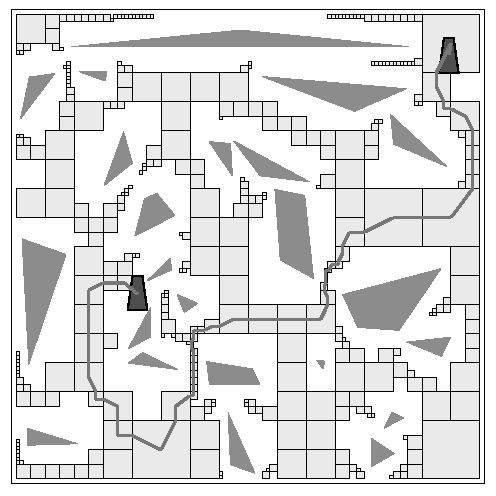
Find path with large clearance to obstacles: [Overmars et al.]

How to deal with non-point or non-circular objects?
 [SIMpact
robot simulation system, Stanford]
[SIMpact
robot simulation system, Stanford]
Idea: For a pair of convex objects, keep track of pair of closest features. HOW?
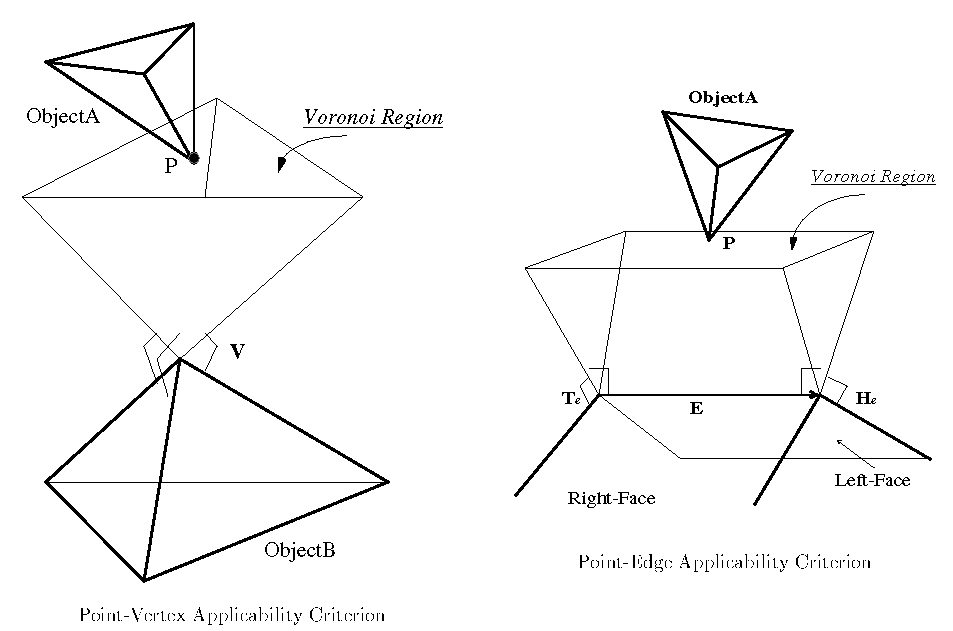
Animation:
Works only for convex objects. Generalization to non-convex objects.
Use with point location in Voronoi cells.

 |
 |
 |
 |
 |
 |
<demo anim1, anim2>