Bézier
Curve and B-Spline Curve
1. Bézier Curve
1.1 Parabola
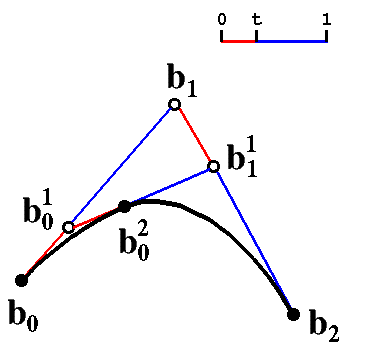
convex combination of the adjacent points
b01(t)
= (1-t) b0 + t b1
b11(t)
= (1-t) b1 + t b2
t in [0, 1]
make convex combination once again
b02(t)=(1-t)b01(t)
+ b11(t)
point b02
goes along a curve from
b0 to b2
explicit form of curve b0,2 as a function of t (parabola):
b02(t)=(1-t)2
b0 + 2t (1-t)
b1 + t2
b2
1.2 Generalize to
order n Bézier Curve
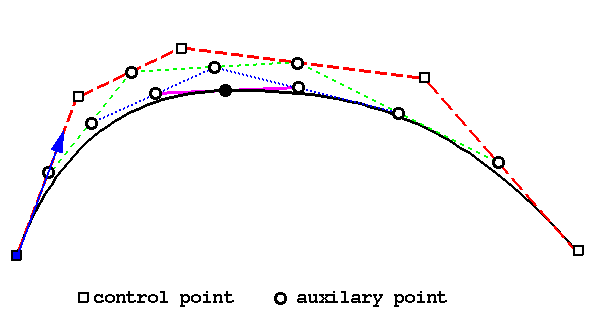
(de Casteljau Algorithm)
Given: points b0 ,b1
, ..., bn, for any
t in [0,1],
set bir
(t) = (1-t) bir-1
(t) + t bi+1r-1
(t)
bi0 (t)
= bi
Then b0n
(t) is the point with parameter value t on the
Bézier curve bn
.
The polygon P formed by b0,
..., bn is called
the Bézier
polygon, or control polygon of curve bn
.
de Casteljau scheme
b0
b1 b01
b2 b11
b02
b3 b21
b12
b03
1.3
Explicit form of Bézier Curve
Bézier curve with control points P0
, ..., Pn :

Bernstein Polynomials :


Bernstein
Polynomials, the cubic case (n=3) :

1.4
Properties of Bézier Curve
1.4.1 Convex Hull Property
For t in [0, 1], b0n
(t) lies in the convex hull of the control
polygon. This is because every intermediate point bir
is a
convex combination of points bir-1,
bi+1r-1
.
1.4.2 Endpoint interpolation
control at endpoint
its position,
first derivative,
second derivative, etc
1.4.3 Shape Preservation
1.4.4 Weistrass Theorem
2. B-Spline Curve
2.1 Why Spline ?
2.2
Why Spline in Bézier Form ?
2.3
What is a Spline ?
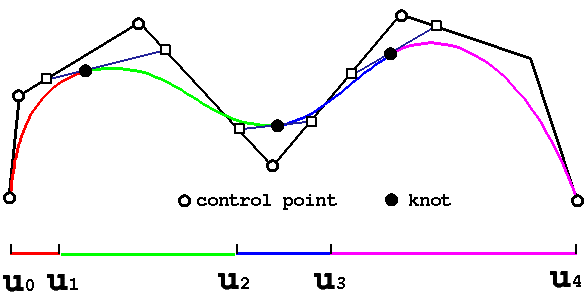
the continuous
map of a collection of intervals into 3-D space .
each interval
is mapped into a polynomial segment.
2.4 C1
and C2 continuity
of B-Spline
C0 continuity(positional): curve
continuous at knot point
C1 continuity(tangental): curve
differentiable at knot point

C2
continuity(curvature): curve doubly differentiable at knot point
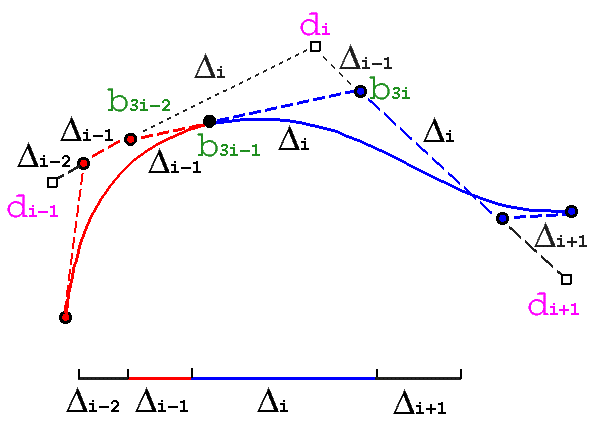
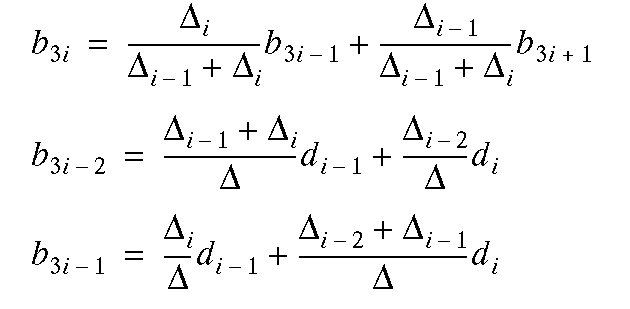
4. NURBS (Non-Uniform Rational
B-Splines)
4.1
Specify a NURB
4.1.1 Control Points and Knots
Control Points : d0
, d1,
..., dL+n-1
Knot sequence (non-decreasing) : u0
, u1,
..., uL+2n-2
B-Spline defined over : [ un-1
, uL+n-1 ]
4.1.2 Explicit Form and Basis Functions





if Knot Sequence becomes : 0,0,0,..,0,1,1,1,...,1
B-Spline basis functions becomes Bernstein Polynomials .
4.2
Rational Spline
 equal weights
equal weights
 non-equal weights
non-equal weights
Specify weights of control points: w0,
w1, ..., wL+n-1










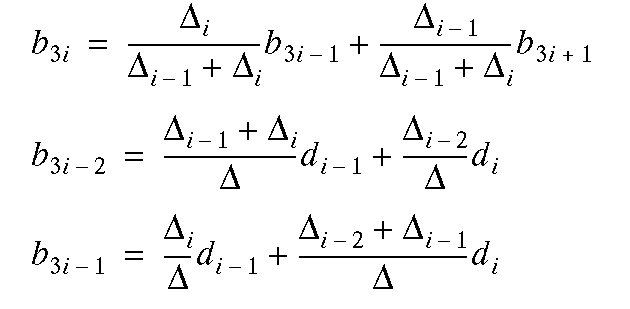





 equal weights
equal weights
 non-equal weights
non-equal weights
