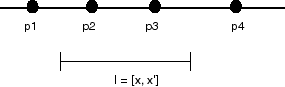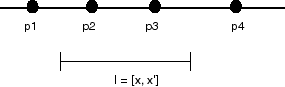1D Binary Searching: a warmup

Resources:

Searching for points on a line:

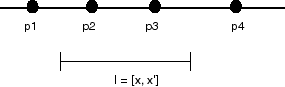
First try: Sort all the points, then scan through the points.  Output all points in the range.
This is O(N), of course we can do better!

Second try: Build a balanced binary search tree, that looks like:

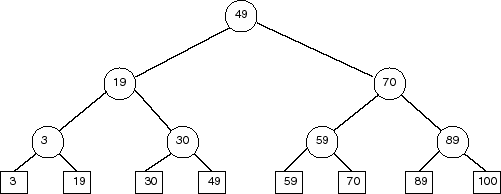
All points stored in the right subtree of a node are greater than the splitting value stored at the node.  All points in the left subtree are less than or equal to the splitting value. To find the points in a given range, proceed as follows:
FindPoints([x, x'], T)
    if T is a leaf node, then
        if x <= val(T) <= x' then
            return { val(T) }
        else
            return {}
        end if
    end if
    <else T is an interior node of tree>
    if x' <= val(T) then
        return FindPoints([x, x'], left(T))
    else if x > val(T) then
        return FindPoints([x, x'], right(T))
    else <interval spans splitting value>
        return FindPoints([x, x'], left(T)) union FindPoints([x, x'], right(T))
    end if

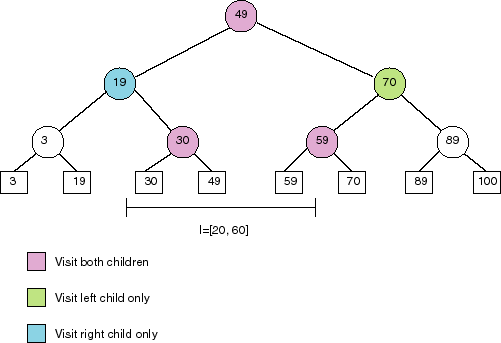
Time complexity: This search takes O(log n + k) when there are k values in the interval, and n values in total.

How to build? There are two ways to build the tree.

1. Top down: sort all the points, then proceed as follows:
• If there is one point only, return a leaf node with that point.
• If there is more than one point, partition the points about the median into two subsets, and recursively build a tree for each subset. Return a node whose value is the median, and whose left and right children are the two recursively constructed subtrees.
2. Bottom up: again, sort all the points.
• Make a leaf node for each point.
• Group the leaf nodes into pairs, under a parent node (maintain less-than/greater than order).
• Recursively group these nodes into pairs until there is only one node (the root node) left.

Other variations: store the median valued points in the internal nodes.

Searching for intervals on a line:

Input: {I1, I2, I3, IN}, [x, x'] where Ii = [xi, xi']
Output: {Ii | Ii overlaps [x, x']}

If we want to find intervals which overlap with a given point x, use the interval [x, x] as the query interval. In the following diagram, the query interval (marked in purple) overlaps with 4 input intervals (marked in green):

First try: stupid linear tricks....

Second try: Build an interval tree.

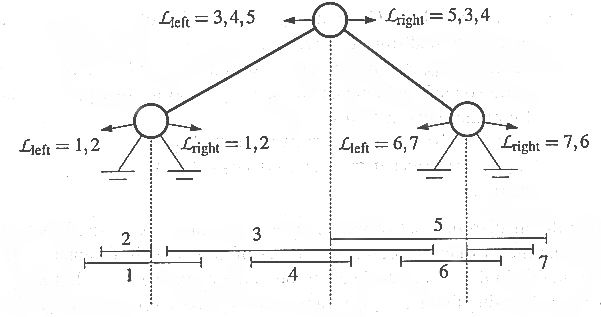
• Partitioning values in this tree are also based on medians, but the median values are taken from the 2N endpoints of all the intervals.
• Left subtrees contain intervals completely to the left of the partitioning value; right subtrees contain intervals completely to the right of the partitioning value.
• Intervals which span the partitioning value of a node are stored at that node; this means we don't have to store an interval multiple times, e.g. when there are lots of overlapping intervals.

Notes:

• These trees can be constructed similarly to the point binary trees.
• There are also variations, e.g. do we push intervals all the way down to the leaf nodes, or do we keep them at internal nodes?

Take home idea: