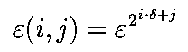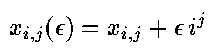Robust Predicates and Degeneracy
6.838 March 16 Meeting
Marek Teichmann
Predicates [Implementations]
See Shewchuk's Robust
Predicates page.
- Point / plane (given by d points) [d+1 x d+1 determinant].
2D: point / line: Area of triangle: 1/6 * det.

3D: point / plane (defined by 3 points)
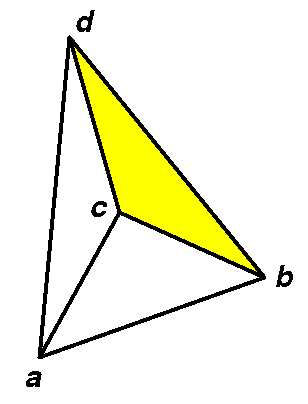 + orientation
if a sees bcd making a left turn.
+ orientation
if a sees bcd making a left turn.
- Point / plane (given by plane equation: replace cx,cy
above by variables, set | | = 0.)
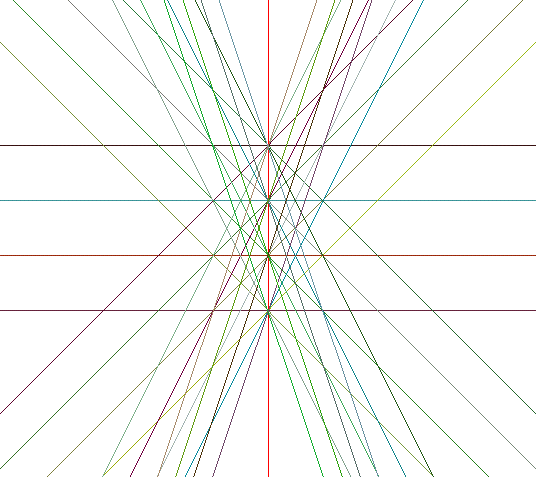 Set of lines with integer coefficients.
Set of lines with integer coefficients.
- Point / sphere (given by d+1 points) [d+2 x d+2
determinant].
2D: point / circle.
FACT: four points (xi,yi) line on a circle
iff (xi,yi,xi2+yi2)
lie on a plane.

IEEE Floating Point Arithmetic.
See: Notes
on IEEE 754 Floating Point Arithmetic (postscript)
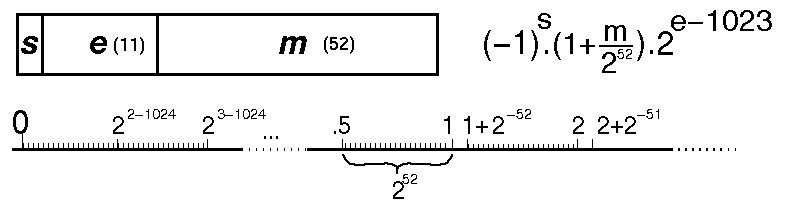
252 numbers between tick marks. Smallest number > 1 is
1 + 2-52.
"Island" of high precision around 0.
fl(1+2-53) = 1
Geometric predicates can FAIL if
implemented in FP.
Predicates implemented using floating point might give wrong answers:
get unexpected or inconsistent state of a program.
Why? Cannot distinguish the two cases below if a = 1:
| orientation | = (a + e) - a
Example: a = 1, e = 2-53: | orientation |
= 0 !
Not invariant w.r.t transformations (a = 0, 1).
Geometric Algorithms.

GEOMETRIC = NUMERIC + COMBINATORIAL
Geometric algorithm : primitive tests on continuous data --> combinatorial
output [Ex. convex hull]
There is a consistency condition between numerical and combinatorial
data.
Can geometric algorithms be implemented using floating point arithmetic?
At all?
Solutions:
- replace arithmetic operations with exact versions
- replace combinatorial part of algorithm to deal with possible errors
in predicates
(make fixed precision computations robust.)
Solution: Exact Arithmetic.
Assumption: input is exact.
Numbers can be represented implicitly.
Evaluate all predicates exactly or up to the required precision (ex.
sign = 1bit).
What kind of numbers [subgroups of R] do we need?
- Integers / fixed point [Clarkson's hull]
- Rational [Avis
& Fukuda's vertex enumeration - Exact LP pivoting]
- Constructible real numbers, real roots of polynomials.
Rational radical expressions: real expressions over the operators +,
-, *, /, sqrt().
- More general (non-algebraic).
Given integer input, what is the smallest class of numbers sufficient
for
- Convex Hull?
- Delaunay Triangulations?
- Intersection of Planes?
- Voronoi Diagram?
- using CH and duality?
- using Fortune's sweep plane algorithm?
Number representations.
See survey by Dube
and Yap (postscript) for survey and references.
Implementation of exact arithmetic: compute every quantity
exactly.
- large integer arithmetic [gnu C++, lea,...]: list of digits (words).
- rational arithmetic [gnu C++,...]
Numerator / Denominator, gcd.
- arbitrary precision floating point arithmetic:
multiple-digit format:
all digits from LS to MS + exponent
Warning: not all rational
numbers are representable.
- MP [Brent, 1978]
- FM [Smith, 1991]
- MPFUN [Bayley 1993], (Linux): dft for *, Newton for 1/x.
- floating point arithmetic: multiple-term
[Priest, Shewchuk] with non-overlapping bits.
f1 + f2 + ...
+ fn
- algebraic numbers.
a is represented by (P(x),(l,u))
where
P(a)=0
and l<a<u and
no other root of P is in (l,u).
((l,u) is called the
separating interval for a)
Example: sqrt(x) is a root p(x2).
- computer algebra. [Mathematica, Maple]
- lazy arithmetic - see below.
Lazy arithmetic: expression based, precision-driven arithmetic.
Numerical quantities are computed to sufficient precision so that
the geometric predicates return correct values. (Underlying combinatorial
structure is mathematically exact.)
- Fixed rational expressions (ex. determinant): incremental floating
point [Shewchuk].
- Any rational radical expression: Real/Expr [Dube,
Yap], LEDA.
Expression Arithmetic: some fundamental ideas.
Geometric predicates are expressions over input coordinates.
How to speed up exact arithmetic? Avoid computing all
digits.
Must specify desired precision for the expressions: ex. 1 bit = sign.
First idea: evaluate expression in fp, then exactly
if needed [Fortune and van Wyk].
Second idea: divide expression into subexpressions, evaluate
incrementally.
Expression tree:
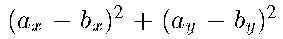

Rational Numbers, finitely representable.
Priest & Shewchuk:
non-overlapping, floating point terms.
Idea: allow roundoff error, but account for it after the
fact by using more terms.
Example: (3 mantissa bit floating point numbers):
101.0011 = 101 + 11. 2-4
Example: 101 + 0.0011 = 101 + roundoff error terms
Operations: +, -, *, /
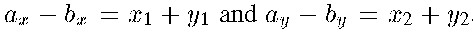
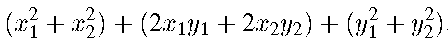
Highest order term is a crude approximation.
Evaluate expression using MST first, then add additional terms as needed.
Algebraic Numbers. Real/Expr,
LEDA
Example: Need to compare an expression to 0.
Need precision bound for root (ex. 1 bit).

1. Propagate precision bound top down (from root to leafs).
Example: a+b: if precision bound for (a+b) is 0.02,
then precision bound for a and b is 0.01.
At each leaf: procedure to extract an approximate value to satisfy precision
bound at the leaf.
2. Propagate value up.
Changing precision bound at root may force (incremental) recomputation.
To how many bits do we need to evaluate an expression to get at
least 1 significant bit?
Example: Graham's
problem:
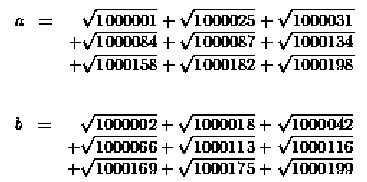
a - b = 0 ? (a=b to 40 digits!!)
Algebraic numbers are roots of polynomials (characteristic polynomial.)
How close is an expression to 0? --> Root bounds.
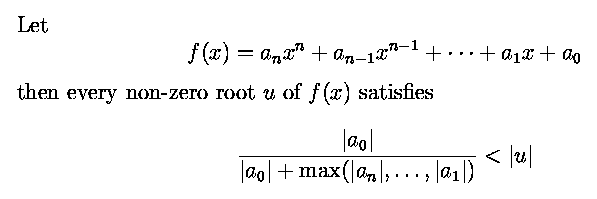
For each node in expression tree maintain
- bigFloat representation
- estimate of algebraic degree and size of coefficients.
Expression tree keeps track of required precision, which is propagated
down the tree to know how precisely a given subexpression (or number) has
to be computed.
Disadvantages: bit size grows, speed about 4 to 10 times
slower than fp.
Packages using exact arithmetic:
Using Finite Precision: Making finite precision predicates robust.
Stability
Definition [Fortune]:
Robustness: A geometric algorithm (using f.p.) is robust
if
- if gives the correct anwer if all primitives give the correct answer.
- no matter what f.p. rounding occurs, the computed answer is the correct
answer for some perturbation of the input.
Stability: An algorithm is stable if it is robust and
the required perturbation is small.
Applications: line arrangements, 2D Delaunay triangulation (get
"almost" delaunay property), convex hull.
Difficulty: careful error analysis of predicates, careful design of algorithm.
Inference of complex predicates from simpler ones.
Predicates : independent and dependent.
- 1. Evaluate independent predicates.
- 2. Use logical consequences of the truth values of the independent
predicates.
(Robustness is separated from error analysis. [Sugihara])

Interval Arithmetic.
[Moore, 1960]
Numbers are represented by an interval 
Interval arithmetic allows computations to be performed on intervals,
such that the result of the computation provides a guaranteed enclosure
for the correct mathematical result over the domain defined by the the
interval operands.
Basic arithmetic operations 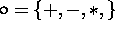 , defined for the the intervals X and Y as all possible
results
, defined for the the intervals X and Y as all possible
results
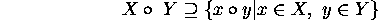
unless 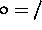 and
and 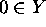 .
.
Example: [a,b] + [c,d] = [a+c, b+d]
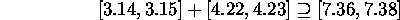
Implementation rounds each interval endpoint outwards.
Predicates can return YES, NO, MAYBE (it is not possible to tell within
precision available.)
Properties: (inclusion isotomy)
- For intervals A,B,C,D, A subset B, C subset D ==> A o C subset
B o D.
- Newton's method works (if the "current interval" becomes
empty, no roots in initial interval.)
- Results corrent when predicates return YES or NO.
Disadvantages:
- - and / are not inverse of + and *
- only sub-distributivity holds: A(B+C) subset AB+AC
about 3 times slower.
Interval geometry
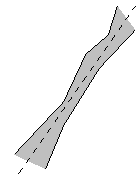 (thick lines) [qhull]
(thick lines) [qhull]
Fatten geometric objects, use tolerancing zones (conservative estimates.)
Predicates can return "don't know".
Topologicaly consistent distortion
 (polylines replace lines)
(polylines replace lines)
Example: Line arrangement construction.
Every intersection between two lines is "snapped" to a grid point.
Rounded geometry
 |
 |
|
representable lines
|
representable points
|
(line coeffs rounded).
Goal: preserve combinatorial structure.
Fact: rounding a collection of disjoint simple polygons while preserving
combinatorial structure is NP-complete.
Discretization
 (pixels)
(pixels)
Epsilon balls
Tolerances / epsilons useful in practice, but no proofs of correctness.
Consider an expression = 0 if |expression| < epsilon.
Tweak until your program works :)
Implicit representations
CSG, Grassman Algebra [Stolfi]
Example: represent a line by 2 points, a point by two lines,...
Ultimately comes down to linear algebra.
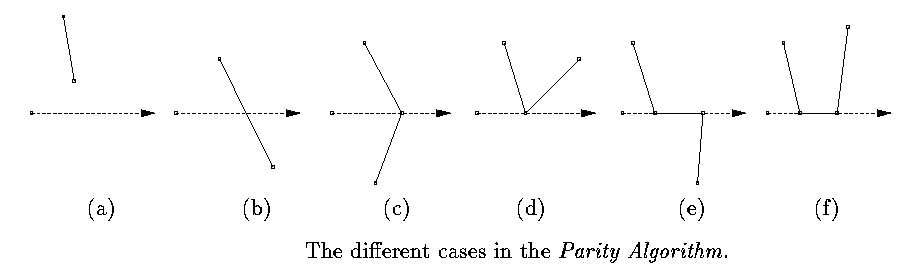
Partity Algorithm: is a point inside or outside a polygon?
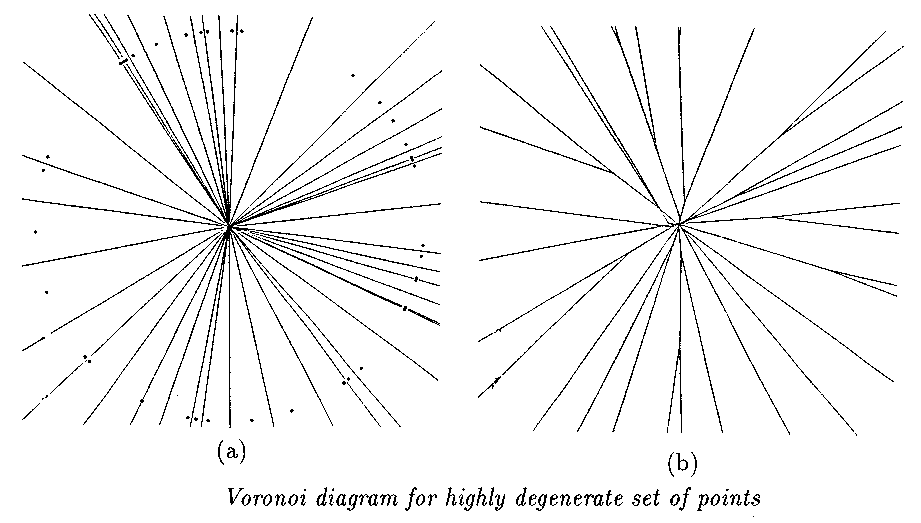
Voronoi Diagram: co-circular points.
Convex Hull: co-planar points. Is a point inside? on a
face? on an edge? on a point?
Def.: A degeneracy occurs when arbitrarily small
perturbation of the input can result in qualitatively different geometric
structures. It is in some sense a discontinuity.
Inherent and algorithm-induced degeneracies.
Ex.: In divide and conquer algorithm for convex hull, colinear points on
convex hull are an inherent degeneracy, collinear points inside are an
induced degeneracy.
What is general position? (Depends on predicates: no predicates return
0).
Perturbation Schemes.
Algorithm working for generic input --> algorithm working
for general input.
General idea:
Let a* be a non-degenerate instance of a problem.
Given a possibly degenerate input instance a, the instance (a +
e a*) is non-degenerate for infinitesimal e.
Trivial perturbation: (ex. sorting)
(xj- xi) ? 0. Want >0 or <0
if xi = xj, return "xi <
xj" iff i<j
Let e = very small number, with (xi+ei)
!= xj for any i,j.
( (xj+ ej) - (xi+ei)
) < 0 if xi = xj and i<j,
General comparisons: xij are variables (i=point
id, j=coordinate).
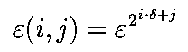
Predicates = polynomials in x's and e's.
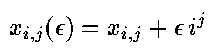 |
 |
|
|
random perturbation |
|
work with `high' probability
|
|
Never compute the values.
Compare x's, then successively higher degrees of e.
Postprocessing.
|
Parity
|
Test query point if on edge |
| Convex hull |
Merge adjacent faces if coplanar
Remove faces subset of larger faces
|
| Voronoi diagram |
Merge Voronoi vertices generated by co-circular points
Remove 0 length edges |
Applications:
- Edelsbrunner and Mucke's 3D delaunay triangulation SOS
- Emiris and Canny's Convex Hull (beneath-beyond algorithm) [perturbation
scheme]

 + orientation
if a sees bcd making a left turn.
+ orientation
if a sees bcd making a left turn. Set of lines with integer coefficients.
Set of lines with integer coefficients.


![[Example of a query]](abc.gif)



 (thick lines) [qhull]
(thick lines) [qhull] (polylines replace lines)
(polylines replace lines)
 (pixels)
(pixels)