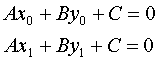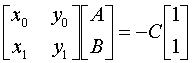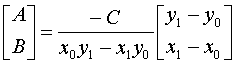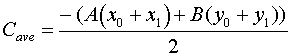Rasterizing Triangles
Triangles are perhaps the most important filled primitive.
Some reasons for this are:
There are two common strategies for scan-converting a triangle.
The first uses edge walking and the second uses edge
equations.
Edge-walking
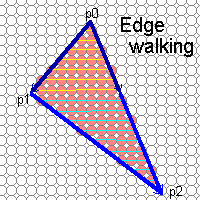 Notes on edge walking:
Notes on edge walking:
- Sort the vertices in both x and y
- Determine if the middle vertex, or breakpoint
lies on the left or right side of the polygon.
If the trianlge has an edge parallel to the scanline
direction then there is no breakpoint.
- Determines the left and right edge for each scanline
(called spans).
- Walk down the left and right edges filling the pixels
in-between until either a breakpoint or the bottom vertex
is reached.
- Exit of change active walking edges.
Advantages and Disadvantages:
- Loaded with special cases
(left and right breakpoints, no breakpoints)
- Difficult to get right
- Requires computing fractional offsets when
interpolating parameters across the triangle
- Generally very fast
The algorithm described in the book is an edge walking algorithm.
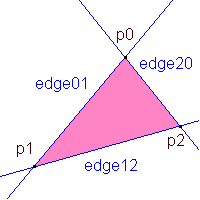
Edge equations
Another approach to rasterizing triangles uses edge equations
to determine which pixels to fill. An edge equation is another
name for the discriminating fuction that we used in our curve
and line-drawing algorithms. An edge equation segments a planar
region into three parts, a boundary, and two half-spaces. The
boundary is identified by points where the edge equation is
equal to zero. The half-spaces are distiguished by differences
in the edge equation's sign. We can choose which half-space
gives a positive sign by multiplication by -1.
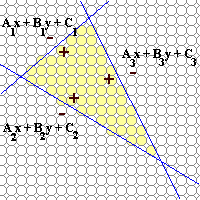 Notes on using edge equations to scan-convert triangles:
Notes on using edge equations to scan-convert triangles:
- Compute edge equations from vertices
- Orient edge equations so that their positive-half
spaces are in the triangle's interior
- Compute a bounding box
- Scan through pixels in bounding box evaluating the
edge equations. When all three are positive then draw
the pixel.
Here's is my example implementation of a triangle rasterizer
that uses edge equations.
Before starting we will define a few useful objects.
First here is the representation of a vertex
public class Vertex2D {
public float x, y; // coordinate of vertex
public int argb; // color of vertex
public Vertex2D(float xval, float yval, int cval)
{
x = xval;
y = yval;
argb = cval;
}
}
Next we define an EdgeEquation object
class EdgeEqn {
public final static int FRACBITS = 12;
public int A, B, C;
public int flag;
public EdgeEqn(Vertex2D v0, Vertex2D v1)
{
double a = v0.y - v1.y;
double b = v1.x - v0.x;
double c = -0.5f*(a*(v0.x + v1.x) + b*(v0.y + v1.y));
A = (int) (a * (1<<FRACBITS));
B = (int) (b * (1<<FRACBITS));
C = (int) (c * (1<<FRACBITS));
flag = 0;
if (A >= 0) flag += 8;
if (B >= 0) flag += 1;
}
public void flip()
{
A = -A;
B = -B;
C = -C;
}
public int evaluate(int x, int y)
{
return (A*x + B*y + C);
}
}
Notice that I'm using integers for my coefficients. This
implementation uses 12 fractional bits, thus its practical
use will be limited to screens with resolutions of 4096 by 4096
or less.
We determine the coefficients of an edge equation using two points
on the edge. Each point determines an equation in terms of our
three unknowns, A, B, and C.
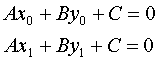
We can solve for A and B in terms of C by setting up the following
homogeneous linear system.
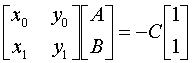
Multiplying both sides by the matrix inverse.
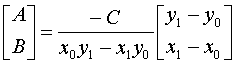
If we choose 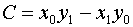 ,
then we get
,
then we get 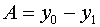 and
and
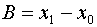 . The equations
for A and B match those that appear in the method
definition.
. The equations
for A and B match those that appear in the method
definition.
In order to understand the expression used for C we'll
need to discuss the numerical precision of the floating point
calculations used by computers. Computers represent floating-point
number internally in a format similar to scientific notation.
Each number is stored with fractional part having a fixed number
of significant digits along with an exponent. If you remember
back to you chemistry or physics classes, the very worse thing
that you can do with numbers represented in scientific notation
is subtract number of similar magnitude. Here is what happens.
Suppose we have four significant digits in our notation. If we
subtract numbers of similar magnitudes as shown below:
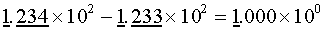
We loose most of the significant digits in our result.
In the case of triangles, we can expect these sort of precision
problems to occur frequently, because in general the vertices
of a triangle are usually relatively close to each other.
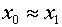 and
and
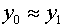 thus
thus
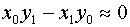
Thankfully, we can avoid this subtraction of large numbers when
computing an expression for C. Given that we know A and
B we can solve for C as follows:
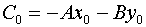 or
or 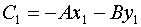
In order to eliminate any unnecessary bias toward either vertex
in our calculation we can compute the average of these C values
as follows.
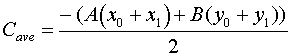
This is the expression for C that appears in our method,
and it avoids many of the numerical problems that plague other
approaches.
The flag is used in computing bounding boxes. We'll consider
that later. Next, let's look at the main loop of the rasterizer.
public class FlatTri implements Drawable {
protected Vertex2D v[];
protected int color;
public FlatTri()
{
}
public FlatTri(Vertex2D v0, Vertex2D v1, Vertex2D v2)
{
v = new Vertex2D[3];
v[0] = v0;
v[1] = v1;
v[2] = v2;
/*
... Our policy is to assign a triangle
the average of it's vertex colors ...
*/
int a = ((v0.argb >> 24) & 255) + ((v1.argb >> 24) & 255) + ((v2.argb >> 24) & 255);
int r = ((v0.argb >> 16) & 255) + ((v1.argb >> 16) & 255) + ((v2.argb >> 16) & 255);
int g = ((v0.argb >> 8) & 255) + ((v1.argb >> 8) & 255) + ((v2.argb >> 8) & 255);
int b = (v0.argb & 255) + (v1.argb & 255) + (v2.argb & 255);
a = (a + a + 3) / 6;
r = (r + r + 3) / 6;
g = (g + g + 3) / 6;
b = (b + b + 3) / 6;
color = (a << 24) | (r << 16) | (g << 8) | b;
}
protected EdgeEqn edge[];
protected int area;
protected int xMin, xMax, yMin, yMax;
private static byte sort[][] = {
{0, 1}, {1, 2}, {0, 2}, {2, 0}, {2, 1}, {1, 0}
};
public void Draw(Raster r)
{
if (!triangleSetup(r)) return;
int x, y;
int A0 = edge[0].A;
int A1 = edge[1].A;
int A2 = edge[2].A;
int B0 = edge[0].B;
int B1 = edge[1].B;
int B2 = edge[2].B;
int t0 = A0*xMin + B0*yMin + edge[0].C;
int t1 = A1*xMin + B1*yMin + edge[1].C;
int t2 = A2*xMin + B2*yMin + edge[2].C;
yMin *= r.width;
yMax *= r.width;
/*
.... scan convert triangle ....
*/
for (y = yMin; y <= yMax; y += r.width) {
int e0 = t0;
int e1 = t1;
int e2 = t2;
int xflag = 0;
for (x = xMin; x <= xMax; x++) {
if ((e0|e1|e2) >= 0) { // all 3 edges must be >= 0
r.pixel[y+x] = color;
xflag++;
} else if (xflag != 0) break;
e0 += A0;
e1 += A1;
e2 += A2;
}
t0 += B0;
t1 += B1;
t2 += B2;
}
}
Most everything here is straight forward, with two exceptions.
- All three edges are tested with a single comparison
by oring together the three edges and checking if the
result is positive. If any one of the thre is negative
then its sign-bit will be set to a 1, and the result of
the or will be negative.
- Since triangles are convex, we can only be inside
for a single interval on any given scanline. The
xflag variable is used to keep track of when we
exit the triangle's interior. If ever we find ourselves
outside of the triangle having already set some pixels
on the span then we can skip over the remainder of the
scanline.
All the dirty work is done by the setup method.
protected boolean triangleSetup(Raster r)
{
if (edge == null) edge = new EdgeEqn[3];
/*
Compute the three edge equations
*/
edge[0] = new EdgeEqn(v[0], v[1]);
edge[1] = new EdgeEqn(v[1], v[2]);
edge[2] = new EdgeEqn(v[2], v[0]);
/*
Trick #1: Orient edges so that the
triangle's interior lies within all
of their positive half-spaces.
Assuring that the area is positive
accomplishes this
*/
area = edge[0].C + edge[1].C + edge[2].C;
if (area == 0) return false; // degenerate triangle
if (area < 0) {
edge[0].flip();
edge[1].flip();
edge[2].flip();
area = -area;
}
/*
Trick #2: compute bounding box
*/
int xflag = edge[0].flag + 2*edge[1].flag + 4*edge[2].flag;
int yflag = (xflag >> 3) - 1;
xflag = (xflag & 7) - 1;
xMin = (int) (v[sort[xflag][0]].x);
xMax = (int) (v[sort[xflag][1]].x + 1);
yMin = (int) (v[sort[yflag][1]].y);
yMax = (int) (v[sort[yflag][0]].y + 1);
/*
clip triangle's bounding box to raster
*/
xMin = (xMin < 0) ? 0 : xMin;
xMax = (xMax >= r.width) ? r.width - 1 : xMax;
yMin = (yMin < 0) ? 0 : yMin;
yMax = (yMax >= r.height) ? r.height - 1 : yMax;
return true;
}
In this method we do two critical things. We orient the
edge equations, and we compute the bounding box.
ToDo: Positive area means positive half spaces.
ToDo: Sorting with the minimum number of compares.
Here is a demonstration of to edge equation based rasterizer
described. Click anywhere below to see an example:
That way easy wasn't it! Go back to the index.
Last updated: Monday, September 30, 1996