At this point the text goes on to discuss ellipse-drawing algorithms. Here I will take a more general approach. You should still read and study the section on drawing ellipses Hearns and Baker pp. 102-110.
Both circles and ellipses are speicial cases of a class of curves known as
conics. Conics are distingished by second-degree descriminating functions
of the form:
Note: this equation (eqn. 3-50, pg. 110) is wrong in the book! (Actually is is just inconsistent with equation 3-51).
The values of the constants, A, B, C, D, E, and F determines the type
of curve as follows:

To make things confusing, mathematicians often refer to the term B2 - 4AC as the conic discriminant. Here we will stick to the computer graphics definition of a discriminant as a function that partitions interior and exterior half-spaces.
Curves of this form arise frequently in phyical simulations, such as plotting the path of a projectile shot from a canon under the influence of gravity (a parabola), or the near collision of like-charged particles (hyperbolas).
Conics, like circles posses symmetry, but not nearly to the same extent. A circle is a very special case of conic, it is so special that it is often considered a non-generic conic. Typically a conic will have only one (parabola) or two (ellipse or hyperbola) symmetric axes. As a result, we won't be able to use the same tricks to avoid slope calculations at each point, that we used when drawing circles.
In order to compute the slope at each point we'll need to find derivatives of
the disccriminating equation:

Using these equations we can compute the instantaneous slope at every point on the conic curve.
The next thing we need is an incremental formulations for the descriminating function
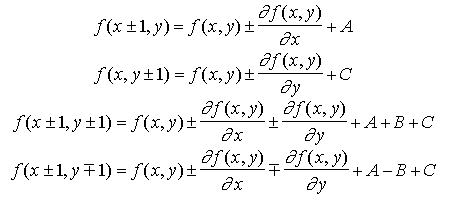
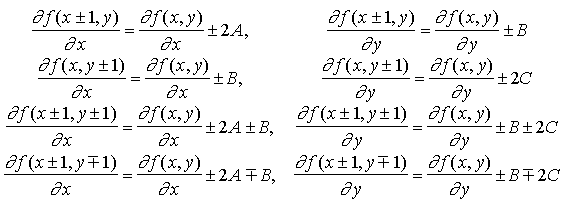
final static int OCTANTS = 0x12650374;
public void conic(
int x0, int y0, // starting point
int x1, int y1, // ending point
Color color, // color of curve
float A, float B, float C, // coefficients of conic
float D, float E, float F)
{
int pix = color.getRGB();
int dxDiag, dyDiag, dxLine, dyLine;
int octant = 0;
float d, u, v;
F = 0;
D = 2*A*x0 + B*y0 + D;
E = B*x0 + 2*C*y0 + E;
if (D >= 0) {
dxDiag = dxLine = 1;
octant += 1;
} else {
dxDiag = dxLine = -1;
}
if (E >= 0) {
dyDiag = dyLine = 1;
octant += 2;
} else {
dyDiag = dyLine = -1;
}
if (Math.abs(E) > Math.abs(D)) {
dxLine = 0;
u = dxDiag*dyDiag*B/2 + C + dyDiag*E;
d = u + A/4 + dxDiag*D/2 + F;
v = u + dxDiag*D;
octant += 4;
} else {
dyLine = 0;
u = dxDiag*dyDiag*B/2 + A + dxDiag*D;
d = u + C/4 + dyDiag*E/2 + F;
v = u + dyDiag*E;
}
octant = (OCTANTS >> (4*octant)) & 7;
float k1 = 2*(A + dyLine*dyDiag*(C - A));
float k2 = dxDiag*dyDiag*B;
float k3 = 2*(A + C + k2);
k2 += k1;
loop: do {
if ((octant & 1) == 0) {
while (2*v <= k2) {
raster.setPixel(pix, x0, y0);
if ((x0 == x1) & (y0 == y1)) break loop;
if (d < 0) {
x0 += dxLine;
y0 += dyLine;
u += k1;
v += k2;
d += u;
} else {
x0 += dxDiag;
y0 += dyDiag;
u += k2;
v += k3;
d += v;
}
}
d = d - u + v/2 - k2/2 + 3*k3/8;
u = -u + v - k2/2 + k3/2;
v = v - k2 + k3/2;
k1 = k1 - 2*k2 + k3;
k2 = k3 - k2;
int t = dxLine; dxLine = -dyLine; dyLine = t;
} else {
while (2*u < k2) {
raster.setPixel(pix, x0, y0);
if ((x0 == x1) & (y0 == y1)) break loop;
if (d > 0) {
x0 += dxLine;
y0 += dyLine;
u += k1;
v += k2;
d += u;
} else {
x0 += dxDiag;
y0 += dyDiag;
u += k2;
v += k3;
d += v;
}
}
float dk = k1 - k2;
d = d + u - v + dk;
v = 2*u - v + dk;
u = u + dk;
k3 = k3 + 4*dk;
k2 = k1 + dk;
int t = dxDiag; dxDiag = -dyDiag; dyDiag = t;
}
octant = (octant + 1) & 7;
} while (true);
}
Actually the most difficult part of using the conic routine is specifying the desired conic. Directly specifying the coefficients, A, B, C, D, E, and F, is not very intuitive. The following interface was designed for specifying ellipses. The user gives three points, the first two are on the ellipse and the third specifies the intersection of the major and minor axes.
The above applet demonstrates the conic() algorithm. Click and drag with the left button the numbered points to vary the shape of the ellipse. Clicking the right button clears the screen.