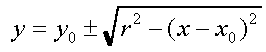Circle-Drawing Algorithms

Beginning with the equation of a circle:
We could solve for y in terms of x
,
and use this equation to compute the pixels of the circle. When finished we'd end up with code that looked something like the following: 
    public void circleSimple(int xCenter, int yCenter, int radius, Color c)
    {
        int pix = c.getRGB();
        int x, y, r2;
        
        r2 = radius * radius;
        for (x = -radius; x <= radius; x++) {
            y = (int) (Math.sqrt(r2 - x*x) + 0.5);
            raster.setPixel(pix, xCenter + x, yCenter + y);
            raster.setPixel(pix, xCenter + x, yCenter - y);
        }
    }
And it would result in circles that look like:
The above applet demonstrates the circleSimple() algorithm. Click and drag the left button to specify the circle's center and a point on its radius. Selecting the right button will clear the drawing. The circle approximation generated by the algorithm is overlaid with an ideal circle for comparison.

As you can see the circles look fine in areas where only one pixel is required for each column, but in areas of the circle where the local slope is greater the one the circle appears discontinuous (where have we seen this before?).

We could take the approach of computing the derivative (i.e. the local slope) of the function at each point and then make a decision whether to step in the x direction or the y direction. But, we will explore a different tact here.

A circle exhibits a great deal of symmetry. We've already exploited this somewhat by plotting two pixels for each function evaluation; one for each possible sign of the square-root function. This symmetry was about the x-axis. The reason that a square-root function brings out this symmetry results from our predilection that the x-axis should be used as an independent variable in function evaluations while the y-axis is dependent. Thus, since a function can yield only one value for member of the domain, we are forced to make a choice between positive and negative square-roots. The net result is that our simple circle-drawing algorithm exploits 2-way symmetry about the x-axis.

Obviously, a circle has a great deal more symmetry. Just as every point above an x-axis drawn through a circle's center has a symmetric point an equal distance from, but on the other side of the x-axis, each point also has a symmetric point on the opposite side of a y-axis drawn through the circle's center.

We can quickly modify our previous algorithm to take advantage of this fact as shown below. 
    public void circleSym4(int xCenter, int yCenter, int radius, Color c)
    {
        int pix = c.getRGB();
        int x, y, r2;
        
        r2 = radius * radius;
        raster.setPixel(pix, xCenter, yCenter + radius);
        raster.setPixel(pix, xCenter, yCenter - radius);
        for (x = 1; x <= radius; x++) {
            y = (int) (Math.sqrt(r2 - x*x) + 0.5);
            raster.setPixel(pix, xCenter + x, yCenter + y);
            raster.setPixel(pix, xCenter + x, yCenter - y);
            raster.setPixel(pix, xCenter - x, yCenter + y);
            raster.setPixel(pix, xCenter - x, yCenter - y);
        }
    }
This circle-drawing algorithm uses 4-way symmetry.
The above applet demonstrates the circleSym4() algorithm. Click and drag the left button to specify the circle's center and a point on its radius. Selecting the right button will clear the drawing. The circle approximation generated by the algorithm is overlaid with an ideal circle for comparison.

This algorithm has all the problems of our previous algorithm, but, it gives the same result with half as many function evaluations. So much for "making it work first" before optimizing. But, we're on a roll so let's push this symmetry thing as far as it will take us.

Notice also that a circle exhibits symmetry about the pair of lines with slopes of one and minus one, as shown below.

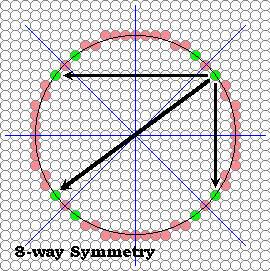
We can find any point's symmetric complement about these lines by permuting the indices. For example the point (x,y) has a complementary point (y,x) about the linex=y. And the total set of complements for the point (x,y) are

The following routine takes advantage of this 8-way symmetry. 

    public void circleSym8(int xCenter, int yCenter, int radius, Color c)
    {
        int pix = c.getRGB();
        int x, y, r2;

        r2 = radius * radius;
        raster.setPixel(pix, xCenter, yCenter + radius);
        raster.setPixel(pix, xCenter, yCenter - radius);
        raster.setPixel(pix, xCenter + radius, yCenter);
        raster.setPixel(pix, xCenter - radius, yCenter);

        y = radius;
        x = 1;
        y = (int) (Math.sqrt(r2 - 1) + 0.5);
        while (x < y) {
            raster.setPixel(pix, xCenter + x, yCenter + y);
            raster.setPixel(pix, xCenter + x, yCenter - y);
            raster.setPixel(pix, xCenter - x, yCenter + y);
            raster.setPixel(pix, xCenter - x, yCenter - y);
            raster.setPixel(pix, xCenter + y, yCenter + x);
            raster.setPixel(pix, xCenter + y, yCenter - x);
            raster.setPixel(pix, xCenter - y, yCenter + x);
            raster.setPixel(pix, xCenter - y, yCenter - x);
            x += 1;
            y = (int) (Math.sqrt(r2 - x*x) + 0.5);
        }
        if (x == y) {
            raster.setPixel(pix, xCenter + x, yCenter + y);
            raster.setPixel(pix, xCenter + x, yCenter - y);
            raster.setPixel(pix, xCenter - x, yCenter + y);
            raster.setPixel(pix, xCenter - x, yCenter - y);
        }
    }
So now we get 8 points for every function evaluation, and this routine should be approximately 4-times faster than our initial circle-drawing algorithm. What's going on with the four pixels that are set outside the loop (both at the top and bottom)? Didn't I say that every point determines 7 others?
The above applet demonstrates the circleSym4() algorithm. Click and drag the left button to specify the circle's center and a point on its radius. Selecting the right button will clear the drawing. The circle approximation generated by the algorithm is overlaid with an ideal circle for comparison.
Wait a Minute!
What has happened here?

It seems suddenly that our circle's appear continuous, and we added no special code to test for the slope. Symmetry has come to our rescue (actually, symmetry is also what saved us on lines... think about it).

So our next objective is to simplify the function evaluation that takes place on each iteration of our circle-drawing algorithm. All those multiplies and square-root evaluations are expensive. We can do better.

One approach is to manipulate of circle equation slightly. First, we translate our coordinate system so that the circle's center is at the origin (the book leaves out this step), giving:

Next, we simplify and make the equation homogeneous (i.e. independent of a scaling of the independent variables; making the whole equation equal to zero will accomplish this) by subtracting r2 from both sides.
We can regard this expression as a function in x and y.
Functions of this sort are called discriminating functions in computer graphics. They have the property of partitioning the domain, pixel coordinates in our case, into one of three categories. When f(x,y) is equal to zero the point lies on the desired locus (a circle in this case), when f(x, y) evaluates to a positive result the point lies one one side of the locus, and when f(x,y) evaluates to negative negative it lies on the other side.

What we'd like to do is to use this discriminating function to maintain our trajectory of drawn pixels as close as possible to the desired circle. Luckily, we can start with a point on the circle, (x0, y0+r) (or (0, r) in our adjusted coordinate system). As we move along in steps of x we note that the slope is less than zero and greater than negative one at points in the direction we're heading that are near our known point on a circle. Thus we need only to figure out at each step whether to step down in y or maintain y at each step.

We will proceed in our circle drawing by literally "walking a tight rope". When we find ourselves on the negative side of the discriminating function, we know that we are slightly inside of our circle so our best hope of finding a point on the circle is to continue with y at the same level. If we ever find ourselves outside of the circle (indicated by a positive discriminate) we will decrease our y value in an effort to find a point on the circle. Our strategy is simple. We need only determine a way of computing the next value of the discriminating function at each step.

Consider what the next value of the discriminating function is in the case that there is no change in y.

We can find an incremental method for computing this equation by expanding terms and substituting for x2 + y2 - r2, giving:

Thus when we are inside the circle with a negative discriminant we can incrementally update the discriminant's value by incrementing by 2x + 1.

Suppose instead that we find ourselves outside of the circle, in this case the next value of the descriminant should be:

Again we can expand and substitute to arrive at the following incremental update equation which will be used when we find ourselves outside the circle:
So when we are outside of the circle we must turn back towards it by changing the y value to y - 1. Then we must update the discriminate by 2x - 2y + 2.

All that remains is to compute the initial value for our discriminating function. Our initial point, (0,r), was on the circle. The very next point, (1, r), will be outside if we continue without changing y (why?). However, we'd like to adjust our equation so that we don't make a change in y unless we are more than half way to it's next value. This can be accomplished by initialing the discriminating function to the value at y - 1/2, a point slightly inside of the circle. This is similar to the initial offset that we added to the DDA line to avoid rounding at every step.

Initializing this discriminator to the midpoint between the current y value and the next desired value is where the algorithm gets its name. In the following code the symmetric plotting of points has be separated from the algorithm. 
    private final void circlePoints(int cx, int cy, int x, int y, int pix)
    {
        int act = Color.red.getRGB();
        
        if (x == 0) {
            raster.setPixel(act, cx, cy + y);
            raster.setPixel(pix, cx, cy - y);
            raster.setPixel(pix, cx + y, cy);
            raster.setPixel(pix, cx - y, cy);
        } else 
        if (x == y) {
            raster.setPixel(act, cx + x, cy + y);
            raster.setPixel(pix, cx - x, cy + y);
            raster.setPixel(pix, cx + x, cy - y);
            raster.setPixel(pix, cx - x, cy - y);
        } else 
        if (x < y) {
            raster.setPixel(act, cx + x, cy + y);
            raster.setPixel(pix, cx - x, cy + y);
            raster.setPixel(pix, cx + x, cy - y);
            raster.setPixel(pix, cx - x, cy - y);
            raster.setPixel(pix, cx + y, cy + x);
            raster.setPixel(pix, cx - y, cy + x);
            raster.setPixel(pix, cx + y, cy - x);
            raster.setPixel(pix, cx - y, cy - x);
        }
    }

    public void circleMidpoint(int xCenter, int yCenter, int radius, Color c)
    {
        int pix = c.getRGB();
        int x = 0;
        int y = radius;
        int p = (5 - radius*4)/4;

        circlePoints(xCenter, yCenter, x, y, pix);
        while (x < y) {
            x++;
            if (p < 0) {
                p += 2*x+1;
            } else {
                y--;
                p += 2*(x-y)+1;
            }
            circlePoints(xCenter, yCenter, x, y, pix);
        }
    }
The page last updated Tuesday, September 17, 1996