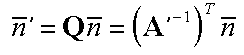
Surface normals are the most important geometric surface characteristic used in computing computer graphics illumination models. The orientation of the surface normal is used in computing both the diffuse and specular components of reflection.
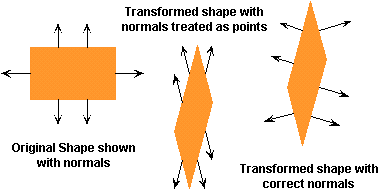
It often comes as a surprise to most individuals that their is any difference between transforming the vertices of an model and the transformation of surface normals. A naive implementer might consider transforming normals by treating them as points offset a unit length from the surface. But even this approach will not work. Consider the following two dimensional example.

The problem with transforming normals occurs when objects undergo an anisotropic scaling (scaling that is not uniform in all directions). Such scaling results only from affine modeling transforms (Why not Euclidean transforms?).
The fundamental problem with transforming normals is largely a product of our mental model of what a normal really is. A normal is not a geometric property relating to points of of the surface, like a quill on a porcupine. Instead normals represent geometric properties on the surface. They are an implicit representation of the tangent space of the surface at a point.
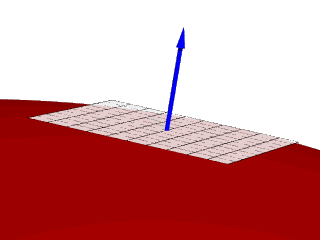
In three dimensions the tangent space at a point is a plane. A plane can be represented by either two basis vectors, but such a representation is not unique. The set of vectors orthogonal to such a plane is, however unique and this vector is what we use to represent the tangent space, and call a normal.
Now that we understand the geometric implications of a normal it is easy to figure out how to transform them.
On a facteted planar surface vectors in the tangent plane can be computed using surface points as follows.
However, not all surfaces are defined as lanar facets. A common example of such a surface is called a parametric surface. For a parametric surface the three-space coordinates are determined by functions of two parameters, u and v in our case.
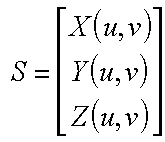
For parametric surfaces two vectors in the tangent plane can be found by computing partial derivitives as follows.
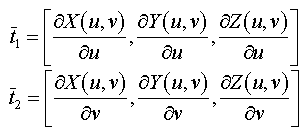
Normals are always orthogonal to the tangent space at a point.
Thus, given two tangent vectors we can compute the normal as follows:
In order to figure out how normals transform, where normals are just an implict representation of the tangent space at a point, we must first consider how transforms affect tangent spaces. The following expression shows an affine transformation of a tangent vector.
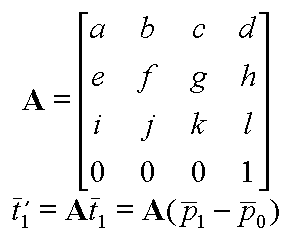
If we multiply this out we get
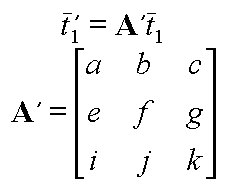
This transoformed tangent, t', must be perpendicular to the transformed normal, n', after that normal undergoes the desired transform Q.
All that we need to do is find a value for the Q matrix so that the transformed normal and the transformed tangent are still orthogonal. This can be accompished by letting
which gives
Thus the transform that must be applied to normals so that they remain perpendicular to the tangent space of transformed points is: